Statistics is a branch of mathematics that involves collecting, analyzing, interpreting, presenting, and organizing data. It is fundamental to making informed decisions and understanding patterns and trends within data. In the context of data science, statistics plays a crucial role, providing the foundation for data analysis, machine learning, and predictive modeling.

Historical Background

Statistics has a rich history, evolving from basic counting methods to complex mathematical theories. The discipline’s roots can be traced back to ancient civilizations, where census data and agricultural statistics were recorded. The formal development of statistics as a mathematical discipline began in the 17th century with the work of pioneers like John Graunt, who analyzed mortality data, and later, Karl Pearson and Ronald Fisher, who laid the groundwork for modern statistical methods.

Types of Statistics

Statistics can be broadly classified into two categories:

1. Descriptive Statistics: These methods summarize and describe the main features of a dataset. Descriptive statistics include measures of central tendency (mean, median, mode) and measures of variability (range, variance, standard deviation).
2. Inferential Statistics: These methods make predictions or inferences about a population based on a sample of data. Inferential statistics include hypothesis testing, confidence intervals, and regression analysis.

Descriptive Statistics

Measures of Central Tendency

1. Mean: The arithmetic average of a dataset. It is calculated by summing all the values and dividing by the number of values.

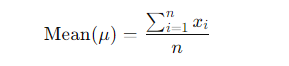
2. Median: The middle value in a dataset when the values are sorted in ascending or descending order. If the dataset has an even number of observations, the median is the average of the two middle numbers.

3. Mode: The value that appears most frequently in a dataset. A dataset can have one mode (unimodal), more than one mode (bimodal or multimodal), or no mode at all.

Measures of Variability

1. Range: The difference between the highest and lowest values in a dataset.

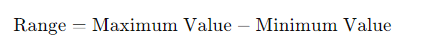
2. Variance: The average of the squared differences from the mean. It provides a measure of how spread out the values are in a dataset.

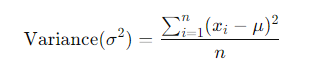
3. Standard Deviation: The square root of the variance. It is expressed in the same units as the data and provides a measure of the average distance from the mean.

Example

Consider a dataset representing the ages of a group of people: [22, 25, 29, 30, 34, 35, 38, 40, 42, 44].

1. Mean:

2. Median: Since the dataset has an even number of values, the median is the average of the 5th and 6th values.

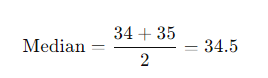
3. Mode: There is no mode as all values are unique.

4. Range:

Range=44−22=22

4. Variance:

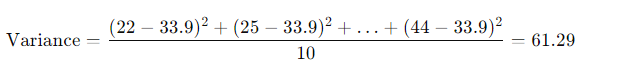
5. Standard Deviation:

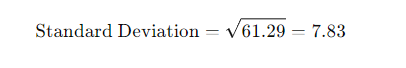
Inferential Statistics

Inferential statistics involve drawing conclusions about a population based on a sample of data. This process includes several key concepts:

Hypothesis Testing

Hypothesis testing is a statistical method used to make inferences or draw conclusions about a population based on sample data. It involves the following steps:

1. Null Hypothesis (H0): A statement that there is no effect or no difference. It is the hypothesis that the researcher seeks to disprove.
2. Alternative Hypothesis (H1): A statement that indicates the presence of an effect or a difference.
3. Test Statistic: A value calculated from the sample data that is used to test the null hypothesis.
4. P-value: The probability of obtaining the observed results, or more extreme results, if the null hypothesis is true. A low p-value (typically less than 0.05) indicates strong evidence against the null hypothesis.
5. Conclusion: Based on the p-value, the null hypothesis is either rejected or not rejected.

Confidence Intervals

A confidence interval is a range of values that is likely to contain the population parameter with a certain level of confidence. For example, a 95% confidence interval for the mean indicates that we are 95% confident that the interval contains the true population mean.

Regression Analysis

Regression analysis is a statistical technique used to model the relationship between a dependent variable and one or more independent variables. The most common form is linear regression, which models the relationship using a linear equation:

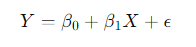
Example

Consider a scenario where a company wants to determine if a new marketing strategy has increased sales. They collect sales data from 30 stores before and after implementing the strategy.

• Null Hypothesis (H0): The new marketing strategy has no effect on sales.
• Alternative Hypothesis (H1): The new marketing strategy has increased sales.

They conduct a paired sample t-test and find a p-value of 0.02. Since the p-value is less than 0.05, they reject the null hypothesis and conclude that the new marketing strategy has significantly increased sales.