Learn Backpropagation Works in Deep Learning
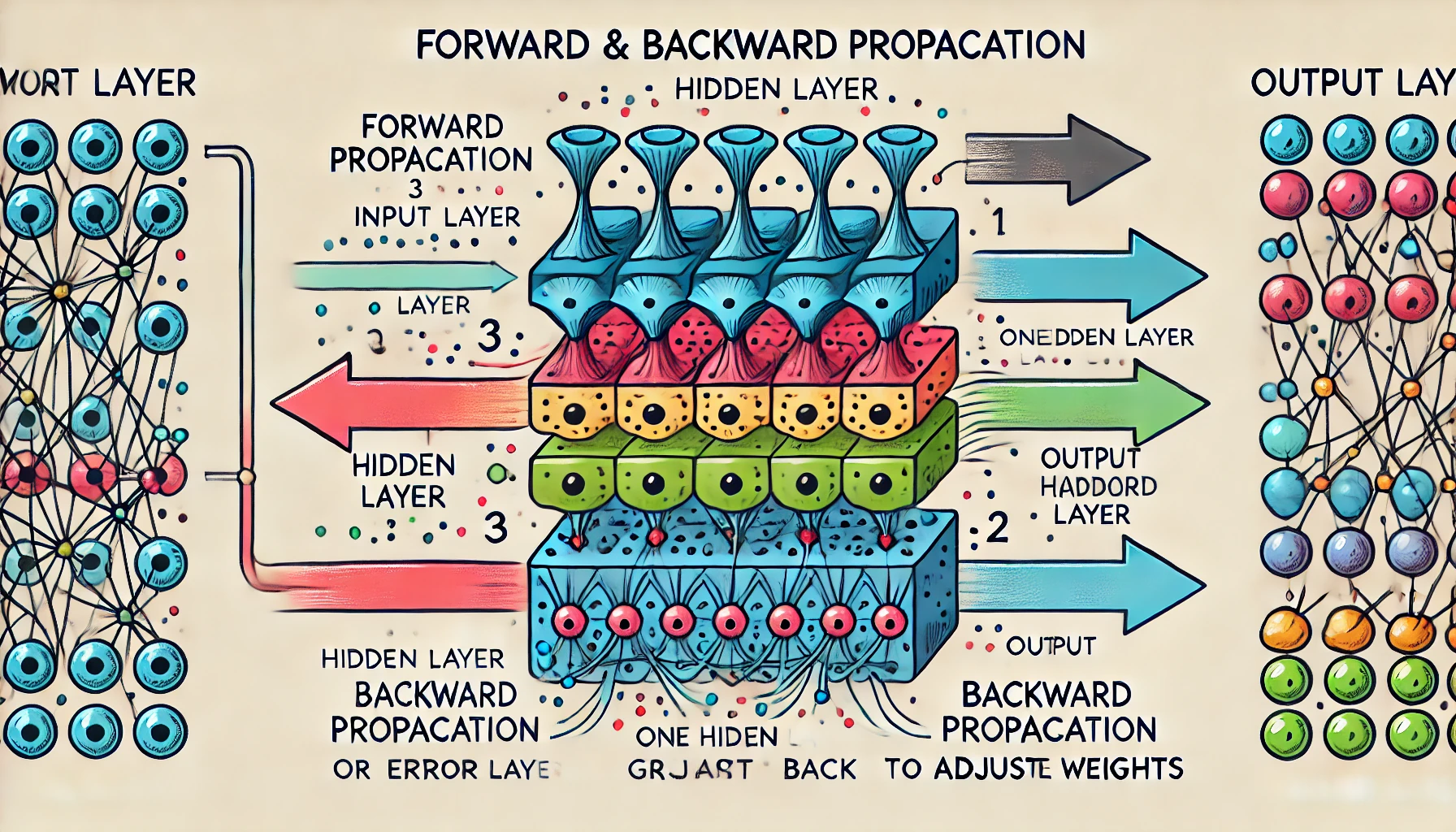
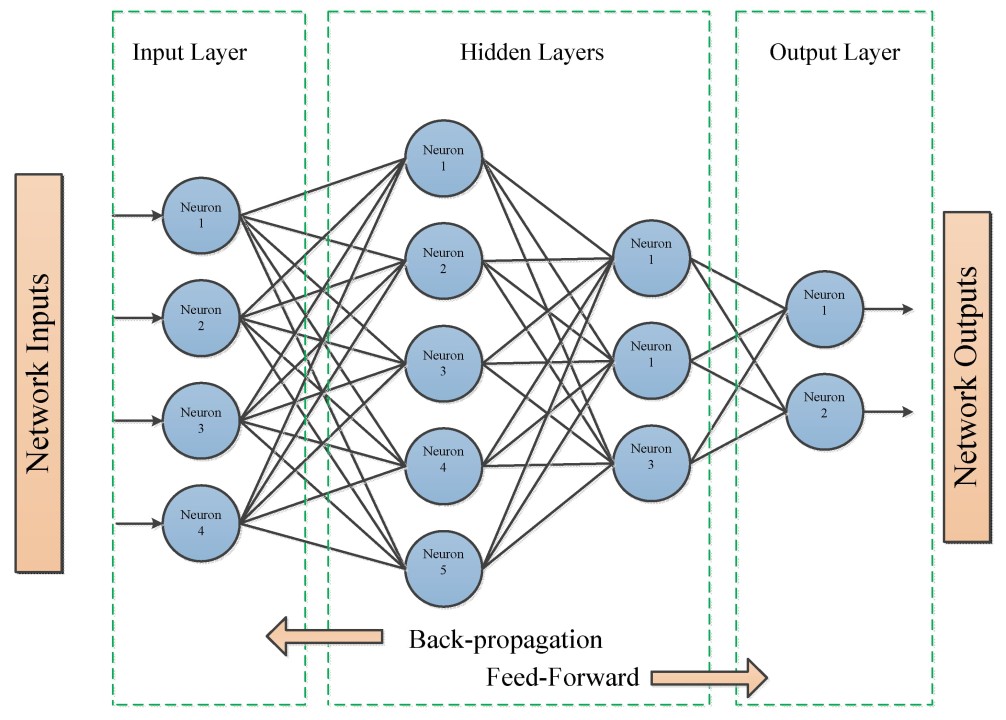
Backpropagation, a cornerstone of neural networks, is an optimization algorithm that enables a model to learn from its errors. The algorithm’s goal is to minimize the error (or “loss”) by updating the model’s weights. It operates in two primary phases: forward propagation and backward propagation.
1. Forward Propagation Overview
In forward propagation, the network processes input data and passes it through each layer of neurons. Each neuron computes a weighted sum of its inputs, adds a bias, and applies an activation function, which shapes the data flowing through the network.
- Example: Suppose we have a simple three-layer neural network (Input → Hidden → Output) trying to predict a binary outcome, like if a patient has a disease based on three features: age, heart rate, and cholesterol level.
- Input Layer: Input neurons receive the feature values (e.g., age = 45, heart rate = 80, cholesterol = 200).
- Hidden Layer: Each neuron here computes a weighted sum of the inputs, applies a bias, and activates it, producing outputs for the next layer.
- Output Layer: After processing through the hidden layer, the data reaches the output neurons, which yield a probability of the patient having the disease.
The network computes a predicted output, say 0.8, representing an 80% likelihood that the patient has the disease.
2. Calculating Error (Loss)
The model’s error (loss) is calculated by comparing the predicted output with the true label (e.g., “has disease = 1”). In this case, if the label is 1, the error is the difference between 1 and 0.8.
3. Backward Propagation
Backpropagation uses this error to update the weights and biases of each neuron, adjusting them to minimize the error on future predictions. Here’s how it works:
-
Gradient Calculation: For each weight, the algorithm calculates the partial derivative of the error with respect to that weight. This derivative (or gradient) tells us how much each weight should change to reduce the error.
-
Weight Update: Using the gradients and a learning rate, each weight is adjusted. Weights leading to larger errors are reduced more significantly.
- Example: Assume that in our network, the error gradients indicate that increasing weight 1 by a small amount reduces the error. The network will then update weight 1 positively to reduce the overall error.
4. Iterative Learning
This process repeats over multiple iterations (epochs), where each epoch gradually reduces the error by adjusting weights, leading to improved accuracy.
Python Code (for clarity)
import numpy as np
# Forward Propagation
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Input values
inputs = np.array([45, 80, 200])
# Weights (initially random)
weights = np.array([0.1, -0.2, 0.3])
# Bias
bias = 0.5
# Forward pass
z = np.dot(inputs, weights) + bias
predicted_output = sigmoid(z)
# Compute error (assuming true label = 1)
true_label = 1
error = predicted_output - true_label
# Backward Propagation
# Calculate gradient
learning_rate = 0.01
gradient = inputs * error * predicted_output * (1 - predicted_output)
# Update weights
weights -= learning_rate * gradient
In this code, the neuron processes input values and updates weights based on the calculated gradient. With multiple epochs, this neuron gradually learns to predict outputs more accurately.
Backpropagation’s main purpose is to reduce prediction error by updating the weights in the neural network. It optimizes the model by adjusting the weights based on the error gradient, allowing it to learn from mistakes.
Forward propagation is the process of passing input data through the network to generate predictions. Backward propagation, on the other hand, adjusts the model’s weights by calculating and minimizing the prediction error.
Activation functions introduce non-linearity into the network, allowing it to learn complex patterns. Without activation functions, a neural network would essentially be a linear model, limiting its ability to solve complex tasks.
The learning rate determines the size of the weight updates during backpropagation. A high learning rate speeds up learning but may cause the model to overshoot the optimal solution, while a low rate may lead to slow learning.
Backpropagation is computationally intensive, especially in large networks with many layers and weights. As the algorithm iteratively adjusts weights, it can significantly increase training time, but optimizations and techniques like mini-batching help speed it up.