Regularization is a crucial concept in data science and statistics, helping to enhance model performance and prevent overfitting. This comprehensive guide explores regularization techniques, their significance, and practical applications in data science.
Table of Contents
- Introduction to Regularization
- Importance of Regularization in Data Science
- Types of Regularization Techniques
- 3.1 Ridge Regression (L2 Regularization)
- 3.2 Lasso Regression (L1 Regularization)
- 3.3 Elastic Net Regularization
- 3.4 Early Stopping
- 3.5 Dropout
- 3.6 Data Augmentation
- Comparison of Regularization Techniques
- Practical Applications and Examples
- Conclusion
1. Introduction to Regularization
Regularization is a set of techniques used to prevent overfitting in machine learning models. Overfitting occurs when a model performs well on training data but poorly on unseen data. Regularization adds a penalty to the model’s complexity, encouraging simpler models that generalize better to new data.
2. Importance of Regularization in Data Science
In data science, the primary goal is to develop models that generalize well to unseen data. Regularization helps achieve this by:
- Reducing model complexity
- Preventing overfitting
- Improving model interpretability
- Enhancing the stability of model predictions
Regularization techniques are essential for both linear models, like linear regression, and more complex models, such as neural networks.
3. Types of Regularization Techniques
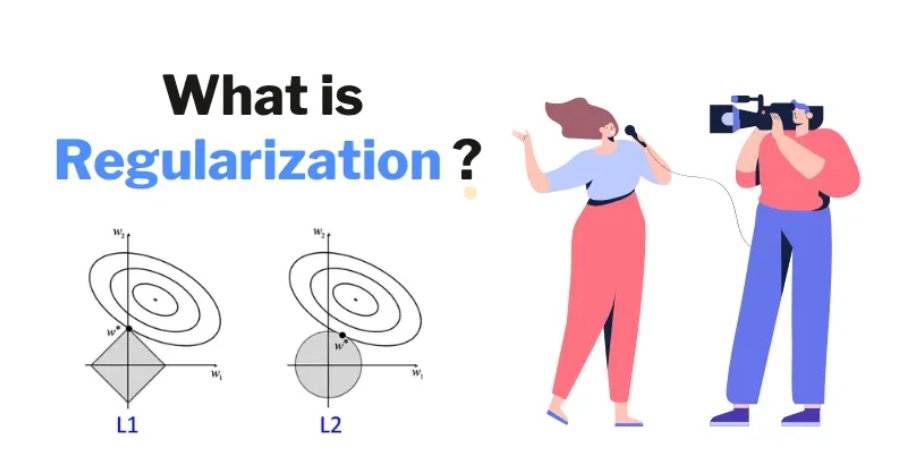
3.1 Ridge Regression (L2 Regularization)
Ridge regression adds a penalty equivalent to the square of the magnitude of coefficients. This technique is particularly useful when there is multicollinearity among the predictor variables.
Mathematical Formulation:

3.2 Lasso Regression (L1 Regularization)
Lasso regression adds a penalty equivalent to the absolute value of the magnitude of coefficients. It can shrink some coefficients to zero, effectively performing variable selection.
Mathematical Formulation:
The objective function with L1 regularization is:

3.3 Elastic Net Regularization
Elastic Net combines both L1 and L2 regularization, inheriting the benefits of both. It is useful when there are multiple correlated features.
Mathematical Formulation:
The objective function for Elastic Net is:

3.4 Early Stopping
Early stopping is a regularization technique used primarily in training neural networks. It involves monitoring the model’s performance on a validation set and stopping training when the performance starts to degrade.
3.5 Dropout
Dropout is a regularization technique used in neural networks where, during training, a random subset of neurons is ignored (dropped out). This prevents neurons from co-adapting too much.
3.6 Data Augmentation
Data augmentation involves increasing the diversity of the training data without actually collecting new data. This can be done by applying random transformations, such as rotations, flips, and crops, to the existing data.
4. Comparison of Regularization Techniques
| Technique | Type of Penalty | Key Benefits | Best Used For |
|---|---|---|---|
| Ridge (L2) | Squared magnitude | Handles multicollinearity well | Linear regression, when features are correlated |
| Lasso (L1) | Absolute magnitude | Feature selection, sparse solutions | Linear regression, high-dimensional data |
| Elastic Net | Combination of L1 & L2 | Balances benefits of L1 and L2 | Scenarios with multiple correlated features |
| Early Stopping | Training interruption | Prevents overfitting in neural networks | Deep learning |
| Dropout | Neuron dropout | Reduces overfitting, improves generalization | Neural networks |
| Data Augmentation | Data transformations | Increases training data diversity | Image and text data |
5. Practical Applications and Examples
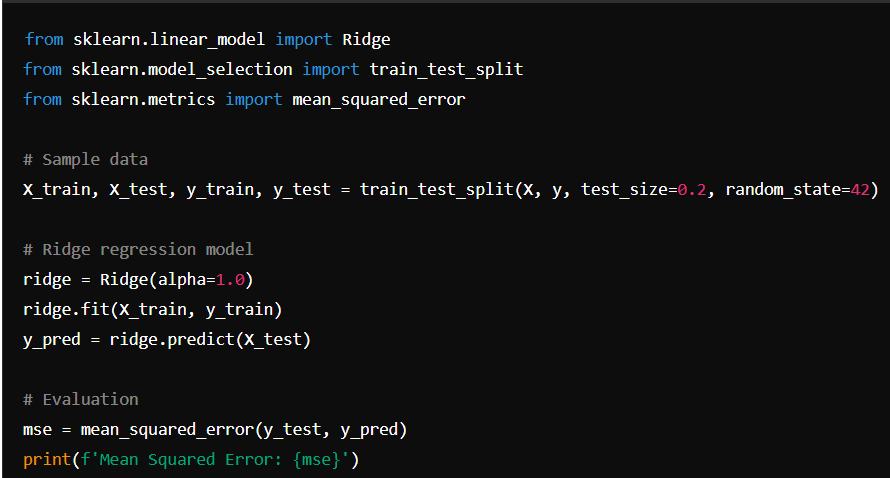
Example 1: Ridge Regression in Python
Example 2: Lasso Regression in Python
Example 3: Elastic Net in Python

6. Conclusion
Regularization techniques are fundamental in data science for developing robust and generalizable models. By incorporating penalties for complexity, regularization helps prevent overfitting and enhances model performance on unseen data. Whether using Ridge, Lasso, Elastic Net, or advanced techniques like early stopping and dropout, understanding and applying regularization is essential for any data scientist.