Bayesian statistics is a powerful and intuitive approach to statistical analysis that incorporates prior knowledge or beliefs into the analysis process. This method contrasts with the frequentist approach, which relies solely on the data at hand. In this blog post, we will delve into the foundations of Bayesian statistics, its key concepts, and its practical applications.

The Bayesian Paradigm

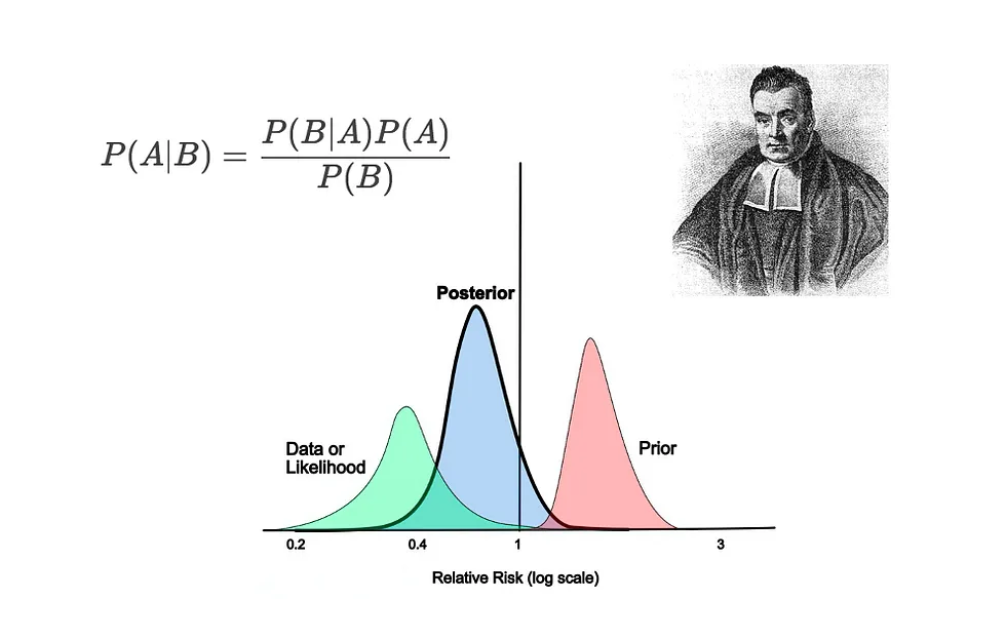
At the heart of Bayesian statistics is Bayes’ Theorem, named after the Reverend Thomas Bayes. Bayes’ Theorem provides a way to update the probability of a hypothesis as more evidence or information becomes available. The theorem is expressed as:

Key Concepts in Bayesian Statistics

1. Prior Distribution: Represents our beliefs about the parameters before seeing the data. This can be based on previous studies, expert knowledge, or subjective judgment.
2. Likelihood: Reflects the plausibility of the observed data under different parameter values. It is derived from the chosen statistical model.
3. Posterior Distribution: The updated beliefs about the parameters after considering the data. This is obtained by combining the prior distribution and the likelihood using Bayes’ Theorem.
4. Bayesian Inference: The process of updating the prior beliefs with the observed data to obtain the posterior distribution.

Benefits of Bayesian Statistics

• Incorporation of Prior Knowledge: Bayesian statistics allows the integration of existing knowledge or expert opinions into the analysis.
• Probability Statements: Provides a direct probability statement about parameters, which is more intuitive and interpretable than the frequentist p-values.
• Flexibility: Can be applied to a wide range of models and is particularly useful for complex hierarchical models.

Practical Applications

Example 1: Bayesian A/B Testing

In A/B testing, we compare two versions of a product to determine which one performs better. Bayesian A/B testing involves setting priors for the conversion rates of both versions and updating these priors with observed data to compute the posterior distributions. This approach allows for continuous monitoring of the test and provides a probability distribution for the effect size.

Example 2: Bayesian Linear Regression

In Bayesian linear regression, we place priors on the regression coefficients and update these priors with the observed data to obtain the posterior distribution of the coefficients. This method provides a full distribution for the estimates, giving more information than point estimates and confidence intervals in frequentist regression.

Implementing Bayesian Statistics

Bayesian analysis can be implemented using various software tools and libraries. Some popular ones include:

• Stan: A probabilistic programming language for specifying statistical models and performing Bayesian inference.
• PyMC3: A Python library for probabilistic programming, which allows users to build and estimate complex Bayesian models.
• JAGS: Just Another Gibbs Sampler, a program for analysis of Bayesian hierarchical models using Markov Chain Monte Carlo (MCMC) simulation.

Conclusion

Bayesian statistics offers a robust framework for incorporating prior knowledge and making probability-based inferences. Its flexibility and intuitive interpretation make it a valuable tool in various fields, from A/B testing to complex hierarchical modeling. By understanding and applying Bayesian methods, data scientists can enhance their analytical capabilities and derive deeper insights from their data.